Interesting problems that I cannot solve
A set of n points in general position in Rd determines
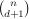simplices. It is always possible to choose a point in Rd, but not necessarily in the set, which lies in a positive proportion of the simplices. How large is this positive proportion? Denote by c(d) the supremum of all c, so that it is possible to choose point in proportion c of all the simplices. Then c(1)=1/2, c(2)=2/9 and 2d/(d+1)(d+1)!≤c(d)≤(d+1)!(d+1)-d-1.
For a graph G let Gp denote the subgraph of G, in which each edge of G is in Gp with probability p independently at random. For any graph H let χ(H) denote the chromatic number of H. Is there a constant c>0 so that E(χ(G1/2))>c χ(G)/log χ(G)?
Since G1/2 and its complement in G have the same distribution, E(χ(G1/2))≥χ(G)1/2. Also, the inequality E(χ(G1/2))>c χ(G)/log n holds, where n is the number of vertices in G.
For a polynomial f in one real variable let T(f) be the number of non-zero terms in f. Is there an ε>0 such that T(f2)≥T(f)ε?
There are polynomials with arbitrarily many terms for which T(f2)≤T(f)99/100. It is known that T(f2)≥(1/100)log T(f).
For a set A⊆Zd and linear maps L1,…,Lk: Zd→Zd define L1A+…+LkA={L1a1+…+Lkak : a1,…,ak∈A}. Suppose L1Zd+…+LkZd=Zd and L1,…,Lk have no common invariant subspace. Does it follow that |L1A+…+LkA|≥[|det L1|1/d+…+|det Lk|1/d]d|A|(1+o(1)) for every finite set A?
The inequality is true if d=1. If A were a closed subset of Rd, then the analogous inequality for the Lebesgue measure would hold by Brunn–Minkowski theorem for every d.
For a graph G, the n'th tensor power G⊗n is the graph with the vertex set V(G)n in which the two vertices (x1,…,xn) and (y1,…,yn) are not adjacent if there is an i for which xi and yi are not adjacent in G. Let C5 denote the 5-cycle graph. Let f(n) be the independence number of C5⊗n. What is the lim f(2n+1)/5n?
Since f(n+2)≥f(2)f(n)=5f(n) the limit exists and is at least 2. Lovász's theta function gives f(n)≤5n/2, and thus the limit is at most √5. Furthermore f(3)=10.
Consider r pairs of points (x1,y1),…,(xr,yr) on a sphere Sn and r continuous functions f1,…,fr:Sn→R. If r is fixed and n is large, is there necessarily a rotation σ∈SO(n+1) such that fi(σxi)=fi(σyi) for all i=1,…,r?
This true for r=1 and for r=2. Then n=1 and n=2 respectively. However, n=r does not suffice in general.
Is there, for every three-element set L⊂Fp and every n, an n-by-n matrix of rank O(n1/3) that has zeros on the diagonal, and elements of L everywhere else?
The simplest open case is {1,4,6} in F19. The n1/3, if attainable, is sharp.
What is the maximum number of n-bit words no two of which have a common subsequence of length 0.501·n?
The number is known to be between log n − O(1) and 2O(logc n).
Is there an algorithm to decide, given an integer polynomial f, if there is a symmetric integer matrix whose characteristic polynomial is a power of f?
The problem is known to be decidable for deg f≤4, but is open even if we restrict to the case deg f=5.
Suppose ℓ1(x),…,ℓt(x) are linear forms whose m'th powers are linearly dependent, and no proper subset thereof has this property. Let L be the linear span of ℓ1,…,ℓt. How large can dim L be?
One has dim L≤cm t + O(1) with cm=3/(m+4) for m≥2. Perhaps, the same holds with cm=1/m? An even more interesting question is to estimate the dimension of the space of t-tuples of linear forms satisfying this condition. The only known way to do so relies on the bounds for dim L, which is rather inefficient.
For d≥3. Let A be a subset of the unit sphere Sd−1 not containing a solution to x+y+z=0. Must it contain at most half of the sphere's measure?
This is known for Rd endowed with the Gaussian measure. For spheres however, it is not even clear that the measure must tend to ½ as d grows.
...but someone else can!
The height of a rational number p/q, where gcd(p,q)=1, is defined to be H(p/q)=|p|+|q|. Suppose f is a real-analytic function on some open interval, which takes rational numbers to rational numbers. Let k be a positive integer. Does H(f(x))≤H(x)k for all rational x imply that f is a rational function with rational coefficients?
I could show this to be true if one assumes that the function f at some point of the domain has Taylor expansion with the first 2k+1 coefficients rational. By theorem 4 in the paper “Rational points near curves and small nonzero |x^3-y^2| via lattice reduction” by Noam Elkies it is always true.
Let P be a set of n points in R2 in general position and L be the set of
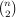lines determined by P. Is it possible that one can choose a collection of O(n) points disjoint from P such that every line in L contains at least one of the points in the collection? A linear lower bound on the size of the collection follows from the fact that no point in the collection can be contained in more than n/2 of the lines. A superlinear lower bound can be deduced from Freiman's theorem under the stronger assumption that the collection contains the midpoint of each of the
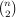line segments. The answer to the question is negative, as shown in “Blocking visibility for points in general position” by Jiří Matoušek, which was pointed to me by David Wood.Let G=(V,E) be a finite graph, and suppose that to each edge e∊E a function fe, from a finite set X to a finite set A, is associated. Let N be the number of functions g: V→X satisfying fxy(g(x))=fxy(g(y)) for every edge xy. If G is the triangle, is there an ε>0 such that N≥|X|3/|A|4-ε?
Imre Ruzsa showed that such an ε does not exist. Let X be a subset of {1,...,n}2 of size |X|=n2-o(1) not containing a corner of the form {(x,y),(x+a,y),(x,y+a)}. Its existence follows from Behrend's construction. Let A={1,...,2n} and put f12(x,y)=x, f13(x,y)=y, f23(x,y)=x+y. If ε>0, for large n we reach a contradiction. Though ε=0, it is possible to prove that w(|A|)N≥|X|3/|A|4 for some function w tending to infinity. If G is a tree, then N≥|X||V|/|A||E|.
For a finite set of integers A define A+A={a+a' : a,a'∈A} and A+2⋅A={a+2a' : a,a'∈A}. Is there an ε>0 such that |A+2⋅A|/|A|≤(|A+A|/|A|)3-ε for all finite sets A?
The inclusion A+2⋅A⊆A+A+A and Plünnecke's inequality together imply that |A+2⋅A|/|A|≤(|A+A|/|A|)3. The problem was answered in affirmative by Hanson and Petridis.
Let f(s)=a1+a22-s+a33-s+… be a Dirichlet series whose coefficients satisfy |an|≤nC. Extend f meromorphically as far as possible. Is the domain of the meromorphic continuation a halfplane?
The question was answered in negative by David Speyer
For an r-uniform hypergraph H and a (r−2)-element set S the link of H over S is the graph {(u,v) : {u,v}∪S∈H}. Let d(r) be the maximum density of an r-uniform hypergraph such that no link contains a copy of K4. Is lim d(r)=0 as r→∞?
Averaging implies that c(2)≥c(3)≥c(4)≥…, and hence the limit exists. I could show that the limit is at most 1/√3. For the analogous question for K3 the limit is zero, with the rate of decay between log r/r2 and 1/r. The analogous question for C4 has negative answer. Surprisingly, the question about K4 was answered by Ellis, Ivan and Leader in negative.
A k-uniform hypergraph is quasirandom if every linearly-sized set U spans (c+o(1))|U|^k edges. For k≥3, give an explicit construction of a k-uniform hypergraph on n-vertices with nk/2 edges.
It turned out this was answered by Alon–Feige–Wigderson–Zuckerman: one can take a regular graph G with small second eigenvalue, and define the hypergraph whose edges are the k-walks. The motivation for the question was that the usual method to show quasirandomness of explicit hypergraphs is via repeated applications of the Cauchy–Schwarz inequality. This method could not succeed with fewer than nk/2+ε edges.
Suppose B1, B2, B3 are three linear bases for Rn. Must there exist three vectors v1, v2, v3 from respective bases that are pairwise nonorthogonal?
Despite being true for orthonormal bases, this turned out to be false. A counterexample was found by Ron Holzman. Denoting +1 and −1 by + and −, the three bases for R4 are B1={+000,+−00,+0+0,++++}, B2={+−−+,0+0−,00++,000+} and B3={00+−,+−+−,++−−,++00}.
