We give a simpler proof of the result of Boros and Füredi
that for any finite set of points in the plane in general
position there is a point lying in 2/9
of all the triangles determined by these points.
Let P be a set of n points in the plane.
By the extension of a theorem of Buck and Buck [3] due
to Ceder [4] there are three concurrent lines
that divide the plane into 6 parts each containing at
least n/6-1 points in its interior. Denote by p the point of
intersection of the three lines. Every choice of six points,
one from each of the six parts, determines a hexagon
containing the point p.
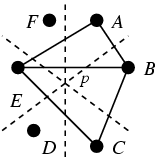 | 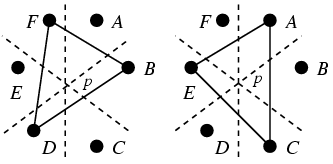 |
| Figure 1: a)p∈ABE or p∈BCE | b)p∈ACE and p∈BDF |
Among the 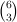 triangles determined by the vertices of the hexagon, at
least 8 triangles contain the point p. Indeed, from each of
the six pairs of triangles situated as in
Figure 1a we get one triangle
containing p. In addition, p is contained in both triangles
of the Figure 1b. Therefore, by double
counting, the number of triangles containing p is at least
triangles determined by the vertices of the hexagon, at
least 8 triangles contain the point p. Indeed, from each of
the six pairs of triangles situated as in
Figure 1a we get one triangle
containing p. In addition, p is contained in both triangles
of the Figure 1b. Therefore, by double
counting, the number of triangles containing p is at least
For the sake of completeness we include a sketch of a proof of the
modification of the theorem of Buck and Buck that we used above.
Proposition 1. Let μ be a finite measure absolutely continuous with respect to
the Lebesgue measure on R2. Then there are
three concurrent lines that partition the plane into
six parts of equal measure.
The partition theorem for the finite set of point P follows
by letting μ be the restriction of the Lebesgue measure
to the union of tiny disks of equal size centered at the
points of P. Since P
is in general position, none of the three lines passes through
more than two of the disks.
Proof sketch. The given measure can be made into one which gives every open
set a strictly positive measure, and which differs little from
the given one. Proving the result for the latter, and using a
compactness argument, one is through. Hence we can assume the
property mentioned, and we normalize the total measure of the
plane to 1.
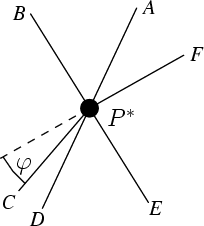 |
| Figure 2: Six rays |
Let now u be a unit vector. There is a unique directed line
L(u)
pointing in the direction u and cutting the plane in two parts of
measure 1/2. For any point P on L(u)
there are six unique rays from P, denoted A(u,P),…,F(u,P) in clockwise order, splitting the
plane in sectors of measure
1/6, with A(u,P) in the direction u. Note that L(u) is the union of
A(u,P) and D(u,P). When P moves along L(u) in the direction u,
the ray B(u,P)
will turn counterclockwise in a continuous way, becoming orthogonal
to L(u) at some point. As the clockwise turning E(u,P) behaves in
the same way, there will be a unique P*(u) such that B(u,P*(u)) and
E(u,P*(u)) form a line.
The line L, the point P* and the six rays from P* clearly depend
continuously on u. In particular the angle
φ(u) one must turn C(u,P*(u))
counterclockwise to complete F(u,P*) to a line varies continuously.
But for any u, we have C(-u,P*(-u))=F(u,P*(u)), and hence
φ(-u)=-φ(u). This shows that for some v the angle
φ(v) vanishes and the rays
C(v,P*(v)) and F(v,P*(v)) form a line. This finishes the proof. □
For no dimension higher than 2 the optimal bounds for C(P,p) are
known. Bárány [1] showed that
there is always a point p for
which C(P,p)≥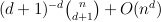 .
.
Acknowledgement. I thank the referee for comments that resulted
in much improved proof of proposition 1.
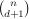 d-simplices. Let p be another point in
Rd. Let C(P,p) be the number of the simplices containing p.
Boros and Füredi [2] constructed a set P of n points in R2 for which
C(P,p)≤
d-simplices. Let p be another point in
Rd. Let C(P,p) be the number of the simplices containing p.
Boros and Füredi [2] constructed a set P of n points in R2 for which
C(P,p)≤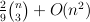 for every point p.
They also proved that there is always a point p for which
C(P,p)≥
for every point p.
They also proved that there is always a point p for which
C(P,p)≥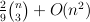 for every point p. Here we present
a new simpler proof of the existence of such a point p.
for every point p. Here we present
a new simpler proof of the existence of such a point p.


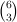 triangles determined by the vertices of the hexagon, at
least 8 triangles contain the point p. Indeed, from each of
the six pairs of triangles situated as in
Figure 1a we get one triangle
containing p. In addition, p is contained in both triangles
of the Figure 1b. Therefore, by double
counting, the number of triangles containing p is at least
triangles determined by the vertices of the hexagon, at
least 8 triangles contain the point p. Indeed, from each of
the six pairs of triangles situated as in
Figure 1a we get one triangle
containing p. In addition, p is contained in both triangles
of the Figure 1b. Therefore, by double
counting, the number of triangles containing p is at least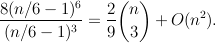

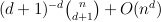 .
.